Tideman

Problème à résoudre

Vous connaissez déjà les élections à la pluralité, qui suivent un algorithme très simple pour déterminer le vainqueur d'une élection : chaque électeur dispose d'une voix, et le candidat qui obtient le plus de voix gagne.

Mais le vote à la pluralité présente quelques inconvénients. Que se passe-t-il, par exemple, lors d'une élection avec trois candidats, et que les bulletins de vote ci-dessous sont exprimés ?

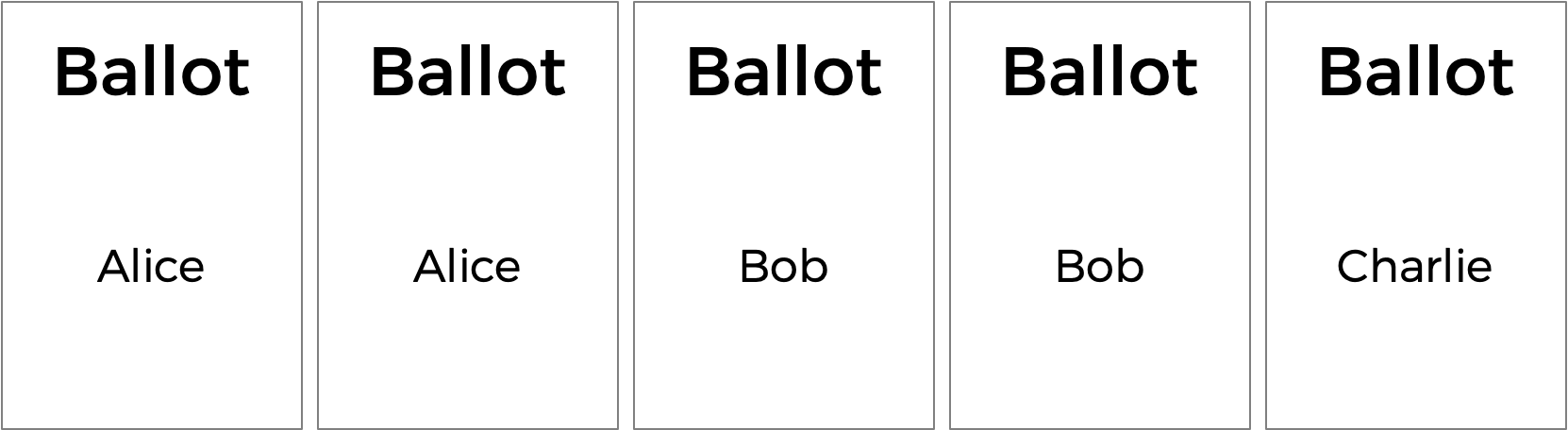
Un vote à la pluralité déclarerait ici une égalité entre Alice et Bob, puisque chacun obtient deux voix. Mais est-ce le bon résultat ?

Il existe un autre type de système de vote appelé système de vote par choix hiérarchisé. Dans un système à choix hiérarchisé, les électeurs peuvent voter pour plus d'un candidat. Au lieu de voter uniquement pour leur premier choix, ils peuvent classer les candidats par ordre de préférence. Les bulletins de vote qui en résultent pourraient donc ressembler à ceux ci-dessous.

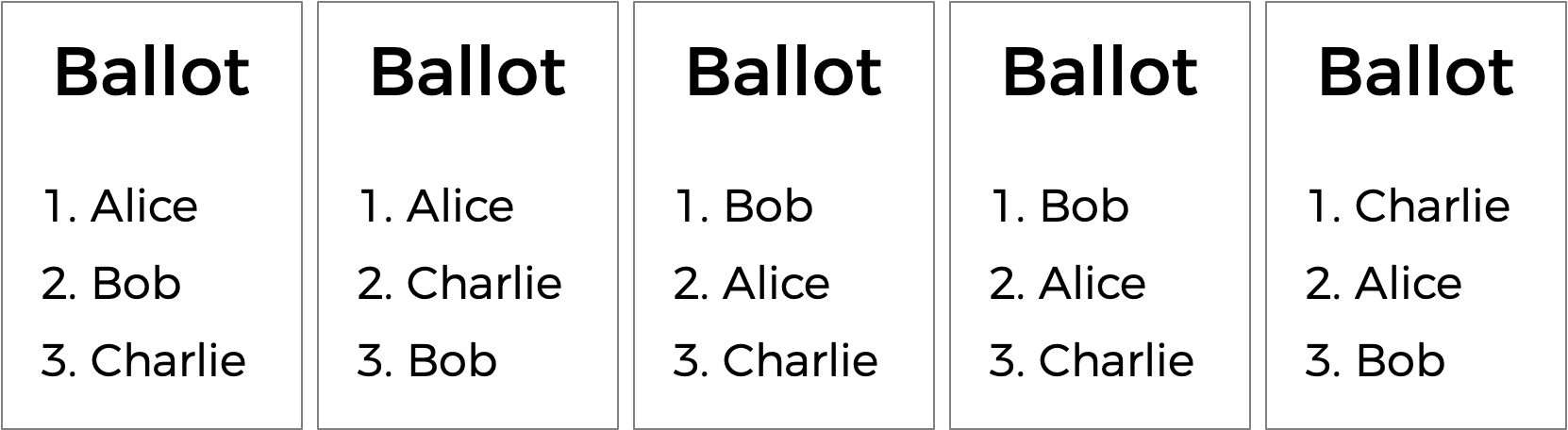
Ici, chaque électeur, en plus de spécifier son candidat de première préférence, a également indiqué ses deuxième et troisième choix. Et maintenant, ce qui était auparavant une élection à égalité pourrait avoir un vainqueur. La course était à l'origine à égalité entre Alice et Bob. Mais l'électeur qui a choisi Charlie a préféré Alice à Bob, donc Alice pourrait ici être déclarée gagnante.

Le vote par choix hiérarchisé peut également résoudre un autre inconvénient potentiel du vote à la pluralité. Examinez les bulletins de vote suivants.

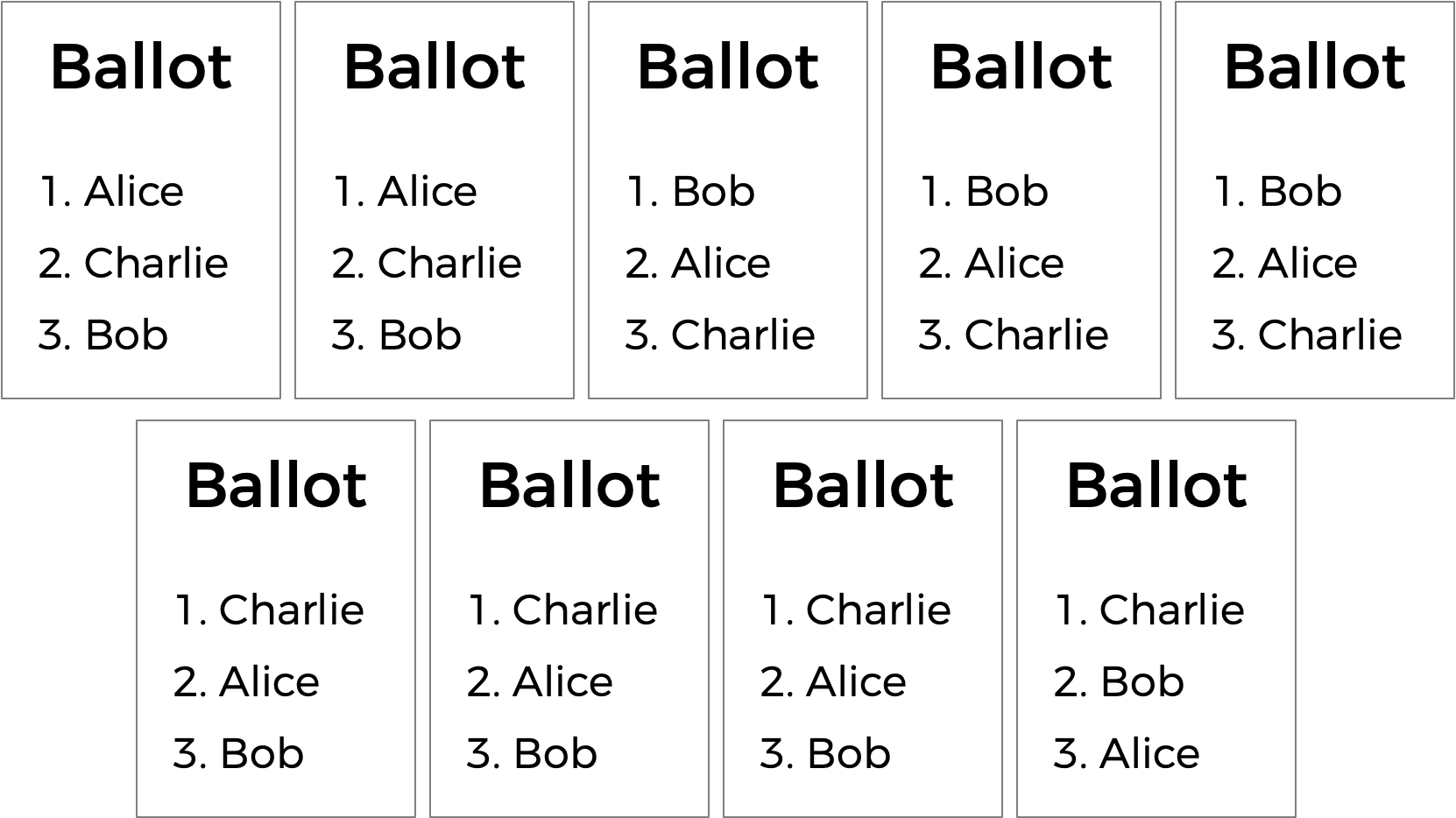
Qui devrait gagner cette élection ? Dans un vote à la pluralité où chaque électeur choisit uniquement sa première préférence, Charlie remporte cette élection avec quatre voix contre seulement trois pour Bob et deux pour Alice. (Notez que, si vous connaissez le système de vote à élimination instantanée, Charlie gagne également ici sous ce système). Alice pourrait cependant raisonnablement faire valoir qu'elle devrait être la gagnante de l'élection au lieu de Charlie : après tout, parmi les neuf électeurs, une majorité (cinq d'entre eux) préférait Alice à Charlie, donc la plupart des gens seraient plus heureux avec Alice comme gagnante plutôt que Charlie.

Alice est, dans cette élection, la soi-disant « gagnante Condorcet » de l'élection : la personne qui aurait remporté n'importe quel affrontement direct contre un autre candidat. Si l'élection n'avait été qu'entre Alice et Bob, ou seulement entre Alice et Charlie, Alice aurait gagné.

La méthode de vote Tideman (également connue sous le nom de « paires classées ») est une méthode de vote par choix hiérarchisé qui garantit de produire le vainqueur Condorcet de l'élection s'il en existe un. Dans un fichier appelé tideman.c dans un dossier appelé tideman, créez un programme pour simuler une élection selon la méthode de vote Tideman.

Démo

Code de distribution

Connectez-vous à cs50.dev, cliquez sur la fenêtre de votre terminal et exécutez cd par lui-même. Vous devriez constater que l'invite de votre fenêtre de terminal ressemble à ce qui suit :

  $

Ensuite, exécutez

  wget https://cdn.cs50.net/2023/fall/psets/3/tideman.zip

afin de télécharger un ZIP appelé tideman.zip dans votre espace de code.

Ensuite, exécutez

  unzip tideman.zip

pour créer un dossier appelé tideman. Vous n'avez plus besoin du fichier ZIP, vous pouvez donc exécuter

  rm tideman.zip

et répondre par « y » suivi d'Entrée à l'invite pour supprimer le fichier ZIP que vous avez téléchargé.

Tapez maintenant

  cd tideman

suivi de la touche Entrée pour vous déplacer (c'est-à-dire ouvrir) dans ce répertoire. Votre invite devrait maintenant ressembler à ce qui suit.

  tideman/ $

Si tout s'est bien passé, vous devez exécuter

  ls

et voir un fichier nommé tideman.c. L'exécution de code tideman.c devrait ouvrir le fichier dans lequel vous taperez votre code pour cet ensemble de problèmes. Sinon, revenez sur vos pas et voyez si vous pouvez déterminer où vous vous êtes trompé !

Contexte

En règle générale, la méthode de Tideman fonctionne en construisant un « graphe » de candidats, où une flèche (c'est-à-dire un bord) du candidat A au candidat B indique que le candidat A gagne contre le candidat B dans un match en tête-à-tête. Dans ce cas, le graphique de l'élection ci-dessus ressemblerait à celui ci-dessous.

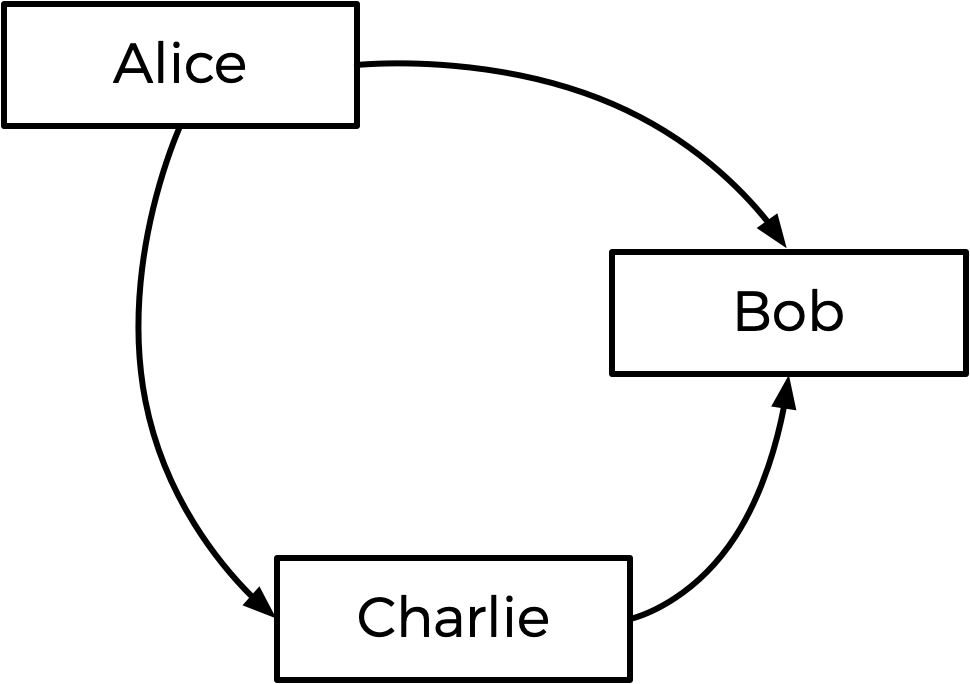
La flèche d'Alice à Bob signifie que plus d'électeurs préfèrent Alice à Bob (5 préfèrent Alice, 4 préfèrent Bob). De même, les autres flèches signifient que plus d'électeurs préfèrent Alice à Charlie, et plus d'électeurs préfèrent Charlie à Bob.

En regardant ce graphique, la méthode Tideman dit que le vainqueur de l'élection devrait être la « source » du graphique (c'est-à-dire le candidat qui n'a aucune flèche pointant vers lui). Dans ce cas, la source est Alice — Alice est la seule à n'avoir aucune flèche pointant vers elle, ce qui signifie que personne n'est préféré à Alice en tête-à-tête. Alice est donc déclarée vainqueur de l'élection.

Il est cependant possible que lorsque les flèches sont tracées, il n'y ait pas de vainqueur de Condorcet. Examinez les bulletins de vote ci-dessous.

Entre Alice et Bob, Alice est préférée à Bob par une marge de 7-2. Entre Bob et Charlie, Bob est préféré à Charlie par une marge de 5-4. Mais entre Charlie et Alice, Charlie est préféré à Alice par une marge de 6-3. Si nous traçons le graphique, il n'y a pas de source ! Nous avons un cycle de candidats, où Alice bat Bob qui bat Charlie qui bat Alice (un peu comme un jeu de pierre-papier-ciseaux). Dans ce cas, il semble qu'il n'y ait aucun moyen de choisir un gagnant.

Pour gérer cela, l'algorithme de Tideman doit veiller à éviter de créer des cycles dans le graphe des candidats. Comment s'y prend-il ? L'algorithme verrouille d'abord les bords les plus forts, car ce sont sans doute les plus importants. En particulier, l'algorithme de Tideman spécifie que les bords de confrontation doivent être « verrouillés » dans le graphique un par un, en fonction de la « force » de la victoire (plus il y a de personnes qui préfèrent un candidat à son adversaire, plus la victoire est forte). Tant que le bord peut être verrouillé dans le graphique sans créer de cycle, le bord est ajouté ; sinon, le bord est ignoré.

Comment cela fonctionnerait-il dans le cas des votes ci-dessus ? Eh bien, la plus grande marge de victoire pour une paire est Alice battant Bob, puisque 7 électeurs préfèrent Alice à Bob (aucun autre affrontement n'a un gagnant préféré par plus de 7 électeurs). Ainsi, la flèche Alice-Bob est d'abord verrouillée dans le graphique. La deuxième plus grande marge de victoire est la victoire de Charlie sur Alice par 6-3, donc cette flèche est verrouillée ensuite.

Vient ensuite la victoire de Bob sur Charlie par 5-4. Mais remarquez : si nous devions ajouter une flèche de Bob à Charlie maintenant, nous créerions un cycle ! Puisque le graphe ne peut pas autoriser de cycles, nous devons ignorer ce bord, et ne pas l'ajouter du tout au graphe. S'il y avait plus de flèches à considérer, nous les examinerions ensuite, mais c'était la dernière flèche, donc le graphe est complet.

Ce processus étape par étape est illustré ci-dessous, avec le graphique final à droite.

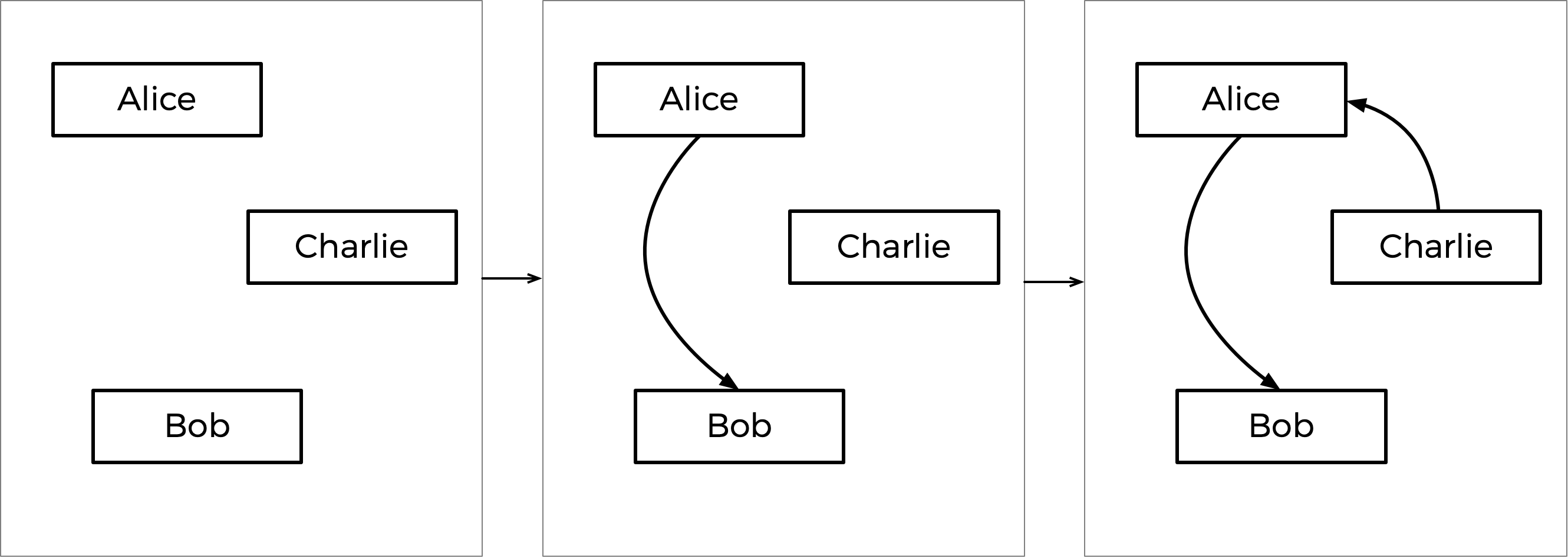
D'après le graphe résultant, Charlie est la source (aucune flèche ne pointe vers Charlie), donc Charlie est déclaré vainqueur de cette élection.

En termes plus formels, la méthode de vote de Tideman comprend trois parties :

• Compte : Une fois que tous les électeurs ont indiqué toutes leurs préférences, déterminez, pour chaque paire de candidats, quel est le candidat préféré et par quelle marge il est préféré.
• Trier : Triez les paires de candidats par ordre décroissant de force de victoire, où la force de victoire est définie comme le nombre d'électeurs qui préfèrent le candidat préféré.
• Verrouiller : En commençant par la paire la plus forte, parcourez les paires de candidats dans l'ordre et « verrouillez » chaque paire dans le graphe des candidats, tant que le verrouillage de cette paire ne crée pas de cycle dans le graphe.

Une fois le graphe terminé, la source du graphe (celle qui n'a aucun bord pointant vers elle) est le gagnant !

Comprendre

Jetons un œil à tideman.c.

Premièrement, remarquez le tableau bidimensionnel preferences. L'entier preferences[i][j] représentera le nombre d'électeurs qui préfèrent le candidat i par rapport au candidat j.

Le fichier définit également un autre tableau bidimensionnel, appelé locked, qui représentera le graphe de candidats. locked est un tableau booléen, donc locked[i][j] étant vrai représente l'existence d'une arête pointant du candidat i vers le candidat j; faux signifie qu'il n'y a pas d'arête. (Si vous êtes curieux, cette représentation d'un graphe est appelée une « matrice d'adjacence »).

Vient ensuite un struct appelé pair, utilisé pour représenter une paire de candidats : chaque paire inclut l'index du candidat gagnant et l'index du candidat perdant.

Les candidats eux-mêmes sont stockés dans le tableau candidates, qui est un tableau de string représentant les noms de chacun des candidats. Il existe également un tableau de pairs, qui représentera toutes les paires de candidats (pour lesquelles l'un est préféré à l'autre) dans l'élection.

Le programme a également deux variables globales : pair_count et candidate_count, représentant respectivement le nombre de paires et le nombre de candidats dans les tableaux pairs et candidates.

Passons maintenant à main. Notez qu'après avoir déterminé le nombre de candidats, le programme boucle sur le graphe locked et définit initialement toutes les valeurs à faux, ce qui signifie que notre graphe initial ne contiendra aucune arête.

Ensuite, le programme boucle sur tous les électeurs et collecte leurs préférences dans un tableau appelé ranks (via un appel à vote), où ranks[i] est l'index du candidat qui a la préférence i pour l'électeur. Ces rangs sont transmis à la fonction record_preference, dont le rôle est de prendre ces rangs et de mettre à jour la variable globale preferences.

Une fois tous les votes enregistrés, les paires de candidats sont ajoutées au tableau pairs via un appel à add_pairs, triées via un appel à sort_pairs, et verrouillées dans le graphe via un appel à lock_pairs. Enfin, print_winner est appelé pour imprimer le nom du gagnant de l'élection !

Plus bas dans le fichier, vous verrez que les fonctions vote, record_preference, add_pairs,sort_pairs, lock_pairs et print_winner sont laissées vides. À vous de jouer !

Spécification

Complétez l'implémentation de tideman.c de manière à simuler une élection de Tideman.

• Complétez la fonction vote.
  • La fonction prend comme arguments rang, nom et rangs. Si nom correspond au nom d'un candidat valide, vous devez mettre à jour le tableau rangs pour indiquer que l'électeur a le candidat comme préférence rang (où 0 est la première préférence, 1 est la deuxième préférence, etc.)
  • Rappelez-vous que rangs[i] représente ici la ième préférence de l'utilisateur.
  • La fonction doit renvoyer vrai si le rang a été enregistré avec succès, et faux sinon (si, par exemple, nom n'est pas le nom de l'un des candidats).
  • Vous pouvez supposer qu'aucun candidat n'aura le même nom.
• Complétez la fonction record_preferences.
  • La fonction est appelée une fois pour chaque électeur, et prend comme argument le tableau rangs, (rappelez-vous que rangs[i] est la ième préférence de l'électeur, où ranks[0] est la première préférence).
  • La fonction doit mettre à jour le tableau global preferences pour ajouter les préférences de l'électeur actuel. Rappelez-vous que preferences[i][j] doit représenter le nombre d'électeurs qui préfèrent le candidat i par rapport au candidat j.
  • Vous pouvez supposer que chaque électeur classera chacun des candidats.
• Complétez la fonction add_pairs.
  • La fonction doit ajouter toutes les paires de candidats où un candidat est préféré au tableau pairs. Une paire de candidats qui sont à égalité (l'un n'est pas préféré à l'autre) ne doit pas être ajoutée au tableau.
  • La fonction doit mettre à jour la variable globale pair_count pour qu'elle soit égale au nombre de paires de candidats. (Les paires doivent donc toutes être stockées entre pairs[0] et pairs[pair_count - 1], inclus).
• Complétez la fonction sort_pairs.
  • La fonction doit trier le tableau pairs par ordre décroissant de force de victoire, où la force de victoire est définie comme le nombre d'électeurs qui préfèrent le candidat préféré. Si plusieurs paires ont la même force de victoire, vous pouvez supposer que l'ordre n'a pas d'importance.
• Complétez la fonction lock_pairs.
  • La fonction doit créer le graphe locked, en ajoutant toutes les arêtes par ordre décroissant de force de victoire tant que l'arête ne créerait pas de cycle.
• Complétez la fonction print_winner.
  • La fonction doit imprimer le nom du candidat qui est la source du graphe. Vous pouvez supposer qu'il n'y aura pas plus d'une source.

Vous ne devez rien modifier d'autre dans tideman.c que les implémentations des fonctions vote, record_preferences, add_pairs, sort_pairs, lock_pairs et print_winner (et l'inclusion de fichiers d'en-tête supplémentaires, si vous le souhaitez). Vous êtes autorisé à ajouter des fonctions supplémentaires à tideman.c, à condition de ne pas modifier les déclarations des fonctions existantes.

Procédure pas à pas

Comment tester

Assurez-vous de tester votre code pour vous assurer qu'il gère :

• Une élection avec n'importe quel nombre de candidats (jusqu'à MAX de 9)
• Voter pour un candidat par son nom
• Votes invalides pour les candidats qui ne sont pas sur le bulletin de vote
• Impression du gagnant de l'élection

Justesse

  check50 cs50/problems/2024/x/tideman

Style

  style50 tideman.c

Comment soumettre

  submit50 cs50/problems/2024/x/tideman