Filtre

Problème à Résoudre

Le moyen le plus simple de représenter une image est peut-être d'utiliser une grille de pixels (c'est-à-dire de points), chacun pouvant être d'une couleur différente. Pour les images en noir et blanc, nous avons donc besoin de 1 bit par pixel, car 0 pourrait représenter le noir et 1 pourrait représenter le blanc, comme indiqué ci-dessous.

En ce sens, une image n'est-elle qu'un bitmap (c'est-à-dire une carte de bits) ? Pour les images plus colorées, vous avez simplement besoin de plus de bits par pixel. Un format de fichier (comme BMP, JPEG ou PNG) qui prend en charge la "couleur 24 bits" utilise 24 bits par pixel. (BMP prend en charge les couleurs 1, 4, 8, 16, 24 et 32 bits.)

Un BMP 24 bits utilise 8 bits pour indiquer la quantité de rouge dans la couleur d'un pixel, 8 bits pour indiquer la quantité de vert dans la couleur d'un pixel et 8 bits pour indiquer la quantité de bleu dans la couleur d'un pixel. Si vous avez déjà entendu parler de la couleur RVB, eh bien, vous l'avez : rouge, vert, bleu.

Si les valeurs R, V et B d'un pixel dans un BMP sont, par exemple, 0xff, 0x00 et 0x00 en hexadécimal, ce pixel est purement rouge, car 0xff (également connu sous le nom 255 en décimal) implique "beaucoup de rouge", tandis que 0x00 et 0x00 impliquent respectivement "pas de vert" et "pas de bleu". Dans ce problème, vous manipulerez ces valeurs R, V et B de pixels individuels, créant ainsi vos propres filtres d'image.

Dans un fichier appelé helpers.c dans un dossier appelé filter-more, écrivez un programme pour appliquer des filtres aux BMP.

Démonstration

Code de distribution

Pour ce problème, vous étendrez les fonctionnalités du code fourni par l'équipe de CS50.

Connectez-vous à cs50.dev, cliquez sur votre fenêtre de terminal et exécutez cd seul. Vous devriez constater que l'invite de votre fenêtre de terminal ressemble à celle-ci :

  $

Exécutez ensuite :

  wget https://cdn.cs50.net/2023/fall/psets/4/filter-more.zip

afin de télécharger un ZIP nommé filter-more.zip dans votre espace de code.

Exécutez ensuite :

  unzip filter-more.zip

pour créer un dossier appelé filter-more. Vous n'avez plus besoin du fichier ZIP, vous pouvez donc exécuter :

  rm filter-more.zip

et répondre par « y » suivi de Entrée à l'invite pour supprimer le fichier ZIP que vous avez téléchargé.

Tapez maintenant :

  cd filter-more

suivi de Entrée pour vous déplacer dans (c'est-à-dire ouvrir) ce répertoire. Votre invite devrait maintenant ressembler à celle-ci :

  filter-more/ $

Exécutez ls seul, et vous devriez voir quelques fichiers : bmp.h, filter.c, helpers.h, helpers.c et Makefile. Vous devriez également voir un dossier appelé images avec quatre fichiers BMP. Si vous rencontrez des problèmes, suivez à nouveau ces mêmes étapes et voyez si vous pouvez déterminer où vous vous êtes trompé !

Contexte

Un peu (mappage de bits) plus technique

N'oubliez pas qu'un fichier est juste une séquence de bits, arrangés d'une certaine façon. Un fichier BMP 24 bits n'est donc essentiellement qu'une séquence de bits, dont (presque) tous les 24 représentent la couleur d'un pixel. Mais un fichier BMP contient également des « métadonnées », des informations telles que la hauteur et la largeur d'une image. Ces métadonnées sont stockées au début du fichier sous la forme de deux structures de données généralement appelées « en-têtes », à ne pas confondre avec les fichiers d'en-tête C. (D'ailleurs, ces en-têtes ont évolué au fil du temps. Ce problème utilise la dernière version du format BMP de Microsoft, 4.0, qui a fait ses débuts avec Windows 95.)

Le premier de ces en-têtes, appelé BITMAPFILEHEADER, a une longueur de 14 octets. (Rappelons que 1 octet équivaut à 8 bits.) Le second de ces en-têtes, appelé BITMAPINFOHEADER, a une longueur de 40 octets. Immédiatement après ces en-têtes se trouve le bitmap réel : un tableau d'octets, dont les triplets représentent la couleur d'un pixel. Cependant, BMP stocke ces triplets à l'envers (c'est-à-dire comme BGR), avec 8 bits pour le bleu, suivis de 8 bits pour le vert, suivis de 8 bits pour le rouge. (Certains BMP stockent également le bitmap entier à l'envers, avec la rangée supérieure d'une image à la fin du fichier BMP. Mais nous avons stocké les BMP de cet ensemble de problèmes comme décrit ici, avec la rangée supérieure de chaque bitmap en premier et la rangée inférieure en dernier.) En d'autres termes, si nous devions convertir le smiley 1 bit ci-dessus en un smiley 24 bits, en remplaçant le noir par du rouge, un BMP 24 bits stockerait ce bitmap comme suit, où 0000ff signifie rouge et ffffff signifie blanc ; nous avons surligné en rouge toutes les instances de 0000ff.

Parce que nous avons présenté ces bits de gauche à droite, de haut en bas, en 8 colonnes, vous pouvez réellement voir le smiley rouge si vous prenez du recul.

Pour être clair, rappelez-vous qu'un chiffre hexadécimal représente 4 bits. En conséquence, ffffff en hexadécimal signifie en réalité 111111111111111111111111 en binaire.

Notez que vous pouvez représenter un bitmap sous la forme d'un tableau de pixels à 2 dimensions : où l'image est un tableau de lignes, chaque ligne est un tableau de pixels. En effet, c'est ainsi que nous avons choisi de représenter les images bitmap dans ce problème.

Filtrage d'image

Que signifie filtrer une image ? On peut considérer le filtrage d'une image comme la prise des pixels d'une image originale, et la modification de chaque pixel de telle sorte qu'un effet particulier soit apparent dans l'image résultante.

Niveaux de gris

Un filtre courant est le filtre « niveaux de gris », où on prend une image et on veut la convertir en noir et blanc. Comment cela fonctionne-t-il ?

Rappelons que si les valeurs rouge, verte et bleue sont toutes définies à 0x00 (hexadécimal pour 0), alors le pixel est noir. Et si toutes les valeurs sont définies à 0xff (hexadécimal pour 255), alors le pixel est blanc. Tant que les valeurs rouge, verte et bleue sont toutes égales, le résultat sera des nuances de gris variables le long du spectre noir et blanc, avec des valeurs plus élevées signifiant des nuances plus claires (plus proches du blanc) et des valeurs plus faibles signifiant des nuances plus foncées (plus proches du noir).

Donc, pour convertir un pixel en niveaux de gris, il suffit de s'assurer que les valeurs rouge, verte et bleue sont toutes de la même valeur. Mais comment savoir quelle valeur leur donner ? Eh bien, il est probablement raisonnable de s'attendre à ce que si les valeurs rouge, verte et bleue d'origine étaient toutes assez élevées, la nouvelle valeur devrait également être assez élevée. Et si les valeurs originales étaient toutes faibles, alors la nouvelle valeur devrait également être faible.

En fait, pour s'assurer que chaque pixel de la nouvelle image a toujours la même luminosité ou la même obscurité que l'ancienne image, on peut prendre la moyenne des valeurs rouge, verte et bleue pour déterminer quelle nuance de gris donner au nouveau pixel.

Si vous appliquez cela à chaque pixel de l'image, le résultat sera une image convertie en niveaux de gris.

Réflexion

Certains filtres peuvent également déplacer les pixels. La réflexion d'une image, par exemple, est un filtre où l'image résultante est ce que vous obtiendriez en plaçant l'image originale devant un miroir. Ainsi, tous les pixels du côté gauche de l'image doivent se retrouver sur la droite, et vice versa.

Notez que tous les pixels originaux de l'image originale seront toujours présents dans l'image réfléchie, c'est juste que ces pixels peuvent avoir été réarrangés pour être à un autre endroit de l'image.

Flou

Il y a plusieurs façons de créer l'effet de flou ou d'adoucissement d'une image. Pour ce problème, nous allons utiliser le « flou gaussien », qui fonctionne en prenant chaque pixel et, pour chaque valeur de couleur, en lui donnant une nouvelle valeur en faisant la moyenne des valeurs de couleur des pixels voisins.

Considérez la grille de pixels suivante, où nous avons numéroté chaque pixel.

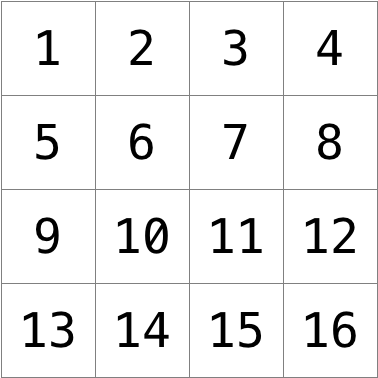
La nouvelle valeur de chaque pixel serait la moyenne des valeurs de tous les pixels qui se trouvent dans une ligne et une colonne de l'image originale (formant une boîte de 3x3). Par exemple, chacune des valeurs de couleur du pixel 6 serait obtenue en faisant la moyenne des valeurs de couleur d'origine des pixels 1, 2, 3, 5, 6, 7, 9, 10 et 11 (notez que le pixel 6 lui-même est inclus dans la moyenne). De même, les valeurs de couleur du pixel 11 seraient obtenues en faisant la moyenne des valeurs de couleur des pixels 6, 7, 8, 10, 11, 12, 14, 15 et 16.

Pour un pixel situé sur le bord ou dans le coin, comme le pixel 15, on chercherait toujours tous les pixels situés dans une ligne et une colonne : dans ce cas, les pixels 10, 11, 12, 14, 15 et 16.

Arêtes

Dans les algorithmes d'intelligence artificielle pour le traitement d'images, il est souvent utile de détecter les arêtes dans une image : des lignes dans l'image qui créent une frontière entre un objet et un autre. Une façon d'obtenir cet effet est d'appliquer l'opérateur de Sobel à l'image.

Tout comme le flou d'image, la détection des arêtes fonctionne également en prenant chaque pixel et en le modifiant en fonction de la grille 3x3 des pixels qui entourent ce pixel. Mais au lieu de simplement prendre la moyenne des neuf pixels, l'opérateur de Sobel calcule la nouvelle valeur de chaque pixel en prenant une somme pondérée des valeurs des pixels environnants. Et puisque les arêtes entre les objets peuvent se produire dans une direction verticale et une direction horizontale, vous calculerez en fait deux sommes pondérées : une pour détecter les arêtes dans la direction x et une pour détecter les arêtes dans la direction y. En particulier, vous utiliserez les deux « noyaux » suivants :

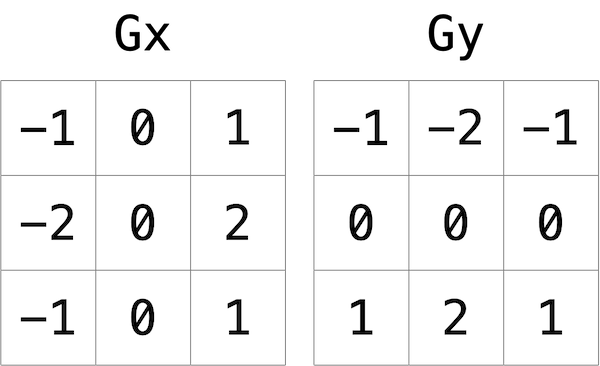
Comment interpréter ces noyaux ? En bref, pour chacune des trois valeurs de couleur de chaque pixel, nous calculerons deux valeurs Gx et Gy. Pour calculer Gx pour la valeur du canal rouge d'un pixel, par exemple, nous prendrons les valeurs rouges d'origine des neuf pixels qui forment une boîte 3x3 autour du pixel, nous les multiplierons chacune par la valeur correspondante dans le noyau Gx, et nous prendrons la somme des valeurs résultantes.

Pourquoi ces valeurs particulières pour le noyau ? Dans la direction Gx, par exemple, nous multiplions les pixels à droite du pixel cible par un nombre positif, et les pixels à gauche du pixel cible par un nombre négatif. Lorsque nous prenons la somme, si les pixels de droite ont une couleur similaire à celle des pixels de gauche, le résultat sera proche de 0 (les nombres s'annulent). Mais si les pixels de droite sont très différents des pixels de gauche, alors la valeur résultante sera très positive ou très négative, indiquant un changement de couleur qui est probablement le résultat d'une frontière entre des objets. Et un argument similaire est valable pour le calcul des arêtes dans la direction y.

À l'aide de ces noyaux, nous pouvons générer une valeur Gx et Gy pour chacun des canaux rouge, vert et bleu d'un pixel. Mais chaque canal ne peut prendre qu'une seule valeur, pas deux : nous avons donc besoin d'un moyen de combiner Gx et Gy en une seule valeur. L'algorithme du filtre de Sobel combine Gx et Gy en une valeur finale en calculant la racine carrée de Gx^2 + Gy^2. Et puisque les valeurs de canal ne peuvent prendre que des valeurs entières de 0 à 255, assurez-vous que la valeur résultante soit arrondie à l'entier le plus proche et plafonnée à 255 !

Et que faire des pixels au bord ou dans le coin de l'image ? Il existe de nombreuses façons de gérer les pixels au bord, mais pour les besoins de ce problème, nous vous demanderons de traiter l'image comme si elle était entourée d'une bordure noire pleine de 1 pixel : par conséquent, essayer d'accéder à un pixel au-delà du bord de l'image doit être traité comme un pixel noir plein (valeurs de 0 pour chaque rouge, vert et bleu). Cela ignorera effectivement ces pixels de nos calculs de Gx et Gy.

Spécification

Implémentez les fonctions dans helpers.c de telle sorte qu'un utilisateur puisse appliquer des filtres de niveaux de gris, de réflexion, de flou ou de détection de contours à ses images.

• La fonction grayscale doit prendre une image et la transformer en une version noir et blanc de la même image.
• La fonction reflect doit prendre une image et la refléter horizontalement.
• La fonction blur doit prendre une image et la transformer en une version floutée (effet « box-blur ») de la même image.
• La fonction edges doit prendre une image et mettre en évidence les contours entre les objets, selon l'opérateur de Sobel.

Vous ne devez modifier aucune des signatures des fonctions, ni aucun autre fichier que helpers.c.

Compréhension

Examinons maintenant certains des fichiers qui vous ont été fournis en tant que code de distribution pour comprendre ce qu'ils contiennent.

bmp.h

Ouvrez bmp.h (en double-cliquant dessus dans le navigateur de fichiers) et examinez-le.

Vous verrez les définitions des en-têtes que nous avons mentionnés (BITMAPINFOHEADER et BITMAPFILEHEADER). En outre, ce fichier définit BYTE, DWORD, LONG et WORD, des types de données que l'on trouve généralement dans le monde de la programmation Windows. Notez qu'ils sont simplement des alias pour des éléments primitifs que vous connaissez (probablement) déjà. Il semble que BITMAPFILEHEADER et BITMAPINFOHEADER utilisent ces types.

Surtout, ce fichier définit également une struct appelée RGBTRIPLE qui, tout simplement, « encapsule » trois octets : un bleu, un vert et un rouge (l'ordre, rappelons-nous, dans lequel nous nous attendons à trouver des triplets RVB sur le disque).

Pourquoi ces struct sont-elles utiles ? Eh bien, rappelez-vous qu'un fichier est simplement une séquence d'octets (ou, en fin de compte, de bits) sur le disque. Mais ces octets sont généralement ordonnés de telle manière que les premiers représentent quelque chose, les suivants représentent autre chose, etc. Les « formats de fichiers » existent parce que le monde a normalisé ce que les octets signifient. Maintenant, nous pourrions simplement lire un fichier à partir du disque dans la RAM comme un grand tableau d'octets. Et nous pourrions simplement nous rappeler que l'octet à array[i] représente une chose, tandis que l'octet à array[j] représente autre chose. Mais pourquoi ne pas donner des noms à certains de ces octets afin que nous puissions les récupérer plus facilement de la mémoire ? C'est précisément ce que les struct dans bmp.h nous permettent de faire. Plutôt que de considérer un fichier comme une longue séquence d'octets, nous pouvons le considérer comme une séquence de struct.

filter.c

Maintenant, ouvrons filter.c. Ce fichier a déjà été écrit pour vous, mais voici quelques points importants à noter :

Premièrement, notez la définition de filters à la ligne 10. Cette chaîne indique au programme quels sont les arguments de ligne de commande autorisés pour le programme : b, e, g et r. Chacun d'eux spécifie un filtre différent que nous pouvons appliquer à nos images : flou, détection des contours, niveaux de gris et réflexion.

Les lignes suivantes ouvrent un fichier image, s'assurent qu'il s'agit bien d'un fichier BMP et lisent toutes les informations sur les pixels dans un tableau 2D appelé image.

Faites défiler jusqu'à l'instruction switch qui commence à la ligne 101. Notez que, selon le filter que nous avons choisi, une fonction différente est appelée : si l'utilisateur choisit le filtre b, le programme appelle la fonction blur ; si e, alors edges est appelée ; si g, alors grayscale est appelée ; et si r, alors reflect est appelée. Notez également que chacune de ces fonctions prend comme arguments la hauteur de l'image, la largeur de l'image et le tableau 2D de pixels.

Voici les fonctions que vous allez (bientôt !) implémenter. Comme vous pouvez l'imaginer, l'objectif est que chacune de ces fonctions modifie le tableau 2D de pixels de manière à ce que le filtre souhaité soit appliqué à l'image.

Les lignes restantes du programme prennent l'image image résultante et l'écrivent dans un nouveau fichier image.

helpers.h

Ensuite, regardez helpers.h. Ce fichier est assez court et fournit simplement les prototypes de fonctions pour les fonctions que vous avez vues précédemment.

Ici, notez que chaque fonction prend un tableau 2D appelé image comme argument, où image est un tableau de height lignes, et chaque ligne est elle-même un autre tableau de width RGBTRIPLE. Donc, si image représente l'image entière, alors image[0] représente la première ligne, et image[0][0] représente le pixel dans le coin supérieur gauche de l'image.

helpers.c

Maintenant, ouvrez helpers.c. C'est ici que l'implémentation des fonctions déclarées dans helpers.h appartient. Mais notez que, pour l'instant, les implémentations sont manquantes ! Cette partie est à vous.

Makefile

Enfin, examinons Makefile. Ce fichier spécifie ce qui doit se produire lorsque nous exécutons une commande de terminal comme make filter. Alors que les programmes que vous avez peut-être écrits auparavant étaient confinés à un seul fichier, filter semble utiliser plusieurs fichiers : filter.c et helpers.c. Nous devrons donc indiquer à make comment compiler ce fichier.

Essayez de compiler filter vous-même en allant à votre terminal et en exécutant :

  $ make filter

Ensuite, vous pouvez exécuter le programme en exécutant :

  $ ./filter -g images/yard.bmp out.bmp

qui prend l'image dans images/yard.bmp et génère une nouvelle image appelée out.bmp après avoir fait passer les pixels dans la fonction grayscale. grayscale ne fait encore rien, donc l'image de sortie devrait ressembler à la cour d'origine.

Astuces

• Les valeurs des composants rgbtRed, rgbtGreen et rgbtBlue d'un pixel sont toutes des entiers, alors assurez-vous d'arrondir tout nombre à virgule flottante à l'entier le plus proche lorsque vous l'assignez à une valeur de pixel !

Procédure pas à pas

Veuillez noter qu'il y a 5 vidéos dans cette playlist.

Comment tester

Assurez-vous de tester tous vos filtres sur les exemples de fichiers bitmap fournis !

Correction

  check50 cs50/problems/2024/x/filter/more

Style

  style50 helpers.c

Comment soumettre

  submit50 cs50/problems/2024/x/filter/more