Leçon 3
Recherche
- La dernière fois, nous avons parlé de la mémoire d'un ordinateur, ou RAM, et comment nos données peuvent être stockées sous forme de variables individuelles ou sous forme de tableaux de plusieurs éléments.
- Nous pouvons considérer un tableau contenant un certain nombre d'éléments comme une rangée de casiers, où un ordinateur ne peut ouvrir qu'un casier à la fois pour examiner un élément.
- Par exemple, si nous voulons vérifier si un nombre se trouve dans un tableau, avec un algorithme qui prend en entrée un tableau et produit un booléen en résultat, nous pourrions : - regarder dans chaque casier, ou dans chaque élément, un à la fois, du début à la fin. - Cela s'appelle recherche linéaire, où nous nous déplaçons en ligne, car notre tableau n'est pas trié. - commencer au milieu et se déplacer à gauche ou à droite en fonction de ce que nous recherchons, si notre tableau d'éléments est trié. - Cela s'appelle recherche binaire, car nous pouvons diviser notre problème en deux à chaque étape, comme ce que David a fait avec l'annuaire téléphonique à la semaine 0.
-
Nous pourrions écrire un pseudo-code pour la recherche linéaire avec :
Pour i de 0 à n-1 Si le i-ème élément est 50 Retourner vrai Retourner faux- Nous pouvons étiqueter chacun des
ncasiers de0àn-1et les cocher chacun dans l'ordre.
- Nous pouvons étiqueter chacun des
-
Pour la recherche binaire, notre algorithme pourrait ressembler à :
Si aucun élément Retourner faux Si l'élément du milieu est 50 Retourner vrai Sinon si 50 < élément du milieu Rechercher dans la moitié gauche Sinon si 50 > élément du milieu Rechercher dans la moitié droite- Éventuellement, il ne nous restera aucune partie du tableau (si l'élément que nous recherchons n'y était pas), nous pouvons donc retourner
faux. - Sinon, nous pouvons rechercher dans chaque moitié en fonction de la valeur de l'élément du milieu.
- Éventuellement, il ne nous restera aucune partie du tableau (si l'élément que nous recherchons n'y était pas), nous pouvons donc retourner
Notation O (grand O)
- Pendant la semaine 0, nous avons vu différents types d'algorithmes et leurs temps d'exécution :
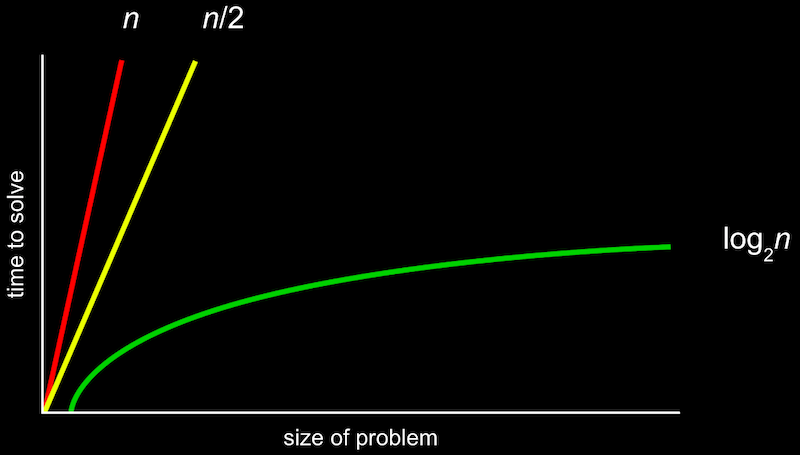
- Une manière plus formelle de décrire cela est d'utiliser la notation O, que nous pouvons comprendre comme « de l'ordre de ». Par exemple, si notre algorithme est une recherche linéaire, il prendra environ O(n) mesures, « de l'ordre de n ». En fait, même un algorithme qui examine deux éléments à la fois et prend n/2 mesures a O(n). En effet, à mesure que n devient de plus en plus grand, seul le terme le plus grand, n, a de l'importance.
- De même, un temps d'exécution logarithmique est O(log n), quelle que soit la base, car il ne s'agit que d'une approximation de ce qui se passe lorsque n est très grand.
- Voici quelques temps d'exécution courants :
- O(n²)
- O(n log n)
- O(n)
- (recherche linéaire)
- O(log n)
- (recherche binaire)
- O(1)
- Les informaticiens peuvent également utiliser la notation Oméga majuscule, qui représente la borne inférieure du nombre d'étapes de notre algorithme. (O majuscule est la borne supérieure du nombre d'étapes, ou le pire des cas, et généralement ce qui nous importe le plus.) Avec la recherche linéaire, par exemple, le pire des cas est de n étapes, mais le meilleur cas est de 1 étape puisque notre élément pourrait être le premier élément que nous vérifions. Le meilleur cas pour la recherche binaire est également de 1, car notre élément peut se trouver au milieu du tableau.
- Et nous avons un ensemble similaire des temps d'exécution Oméga majuscule les plus courants :
- Ω(n²)
- Ω(n log n)
- Ω(n)
- (comptage du nombre d'éléments)
- Ω(log n)
- Ω(1)
- (recherche linéaire, recherche binaire)
Recherche linéaire
-
Jetons un coup d'œil à
numbers.c:#include <cs50.h> #include <stdio.h> int main(void) { // Un tableau de nombres int numbers[] = {4, 8, 15, 16, 23, 42}; // Rechercher 50 for (int i = 0; i < 6; i++) { if (numbers[i] == 50) { printf("Trouvé\n"); return 0; } } printf("Non trouvé\n"); return 1; } -
Ici, nous initialisons un tableau avec quelques valeurs, et nous vérifions les éléments du tableau un par un, dans l'ordre.
-
Et dans chaque cas, selon que la valeur a été trouvée ou non, nous pouvons renvoyer un code de sortie de 0 (pour le succès) ou de 1 (pour l'échec).
-
Nous pouvons faire la même chose pour les noms :
#include <cs50.h> #include <stdio.h> #include <string.h> int main(void) { // Un tableau de noms string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"}; // Rechercher EMMA for (int i = 0; i < 4; i++) { if (strcmp(names[i], "EMMA") == 0) { printf("Trouvé\n"); return 0; } } printf("Non trouvé\n"); return 1; } -
Nous ne pouvons pas comparer directement des chaînes de caractères, car ce ne sont pas des types de données simples mais plutôt un tableau de plusieurs caractères, et nous devons les comparer différemment. Heureusement, la bibliothèque
stringa une fonctionstrcmpqui compare les chaînes de caractères pour nous et renvoie0si elles sont identiques. Nous pouvons donc l'utiliser. -
Essayons d'implémenter un annuaire téléphonique avec les mêmes idées :
#include <cs50.h> #include <stdio.h> #include <string.h> int main(void) { string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"}; string numbers[] = {"617–555–0100", "617–555–0101", "617–555–0102", "617–555–0103"}; for (int i = 0; i < 4; i++) { if (strcmp(names[i], "EMMA") == 0) { printf("Trouvé %s\n", numbers[i]); return 0; } } printf("Non trouvé\n"); return 1; } -
Nous utiliserons des chaînes de caractères pour les numéros de téléphone, car ils peuvent inclure un formatage ou être trop longs pour un nombre.
- Maintenant, si le nom à un certain index dans le tableau
namescorrespond à celui que nous recherchons, nous renverrons le numéro de téléphone dans le tableaunumbers, au même index. Mais cela signifie que nous devons être particulièrement attentifs pour nous assurer que chaque numéro correspond au nom à chaque index, surtout si nous ajoutons ou supprimons des noms et des numéros.
Structures
-
Il s'avère que nous pouvons créer nos propres types de données personnalisés appelés structures :
#include <cs50.h> #include <stdio.h> #include <string.h> typedef struct { string name; string number; } person; int main(void) { person people[4]; people[0].name = "EMMA"; people[0].number = "617–555–0100"; people[1].name = "RODRIGO"; people[1].number = "617–555–0101"; people[2].name = "BRIAN"; people[2].number = "617–555–0102"; people[3].name = "DAVID"; people[3].number = "617–555–0103"; // Recherche EMMA for (int i = 0; i < 4; i++) { if (strcmp(people[i].name, "EMMA") == 0) { printf("Found %s\n", people[i].number); return 0; } } printf("Not found\n"); return 1; } -
Nous pouvons considérer les structures comme des conteneurs, à l'intérieur desquels se trouvent plusieurs autres types de données.
- Ici, nous créons notre propre type avec une structure appelée
personne, qui aura unechaîneappeléenomet unechaîneappeléenuméro. Ensuite, nous pouvons créer un tableau de ces types de structure et initialiser les valeurs à l'intérieur de chacun d'eux, en utilisant une nouvelle syntaxe,., pour accéder aux propriétés de chaquepersonne. - Dans notre boucle, nous pouvons maintenant être plus certains que le
numérocorrespond aunompuisqu'ils proviennent du même élémentpersonne.
Tri
- Si notre entrée est une liste non triée de nombres, il existe de nombreux algorithmes que nous pourrions utiliser pour produire une liste triée en sortie.
- Avec huit volontaires sur scène ayant les numéros suivants, nous pourrions envisager d'échanger les paires de nombres voisins comme première étape.
-
Nos volontaires commencent dans l'ordre aléatoire suivant :
6 3 8 5 2 7 4 1 -
Nous examinons les deux premiers nombres et les échangeons pour qu'ils soient dans l'ordre :
6 3 8 5 2 7 4 1 – – 3 6 8 5 2 7 4 1 -
La paire suivante,
6et8, est dans l'ordre, nous n'avons donc pas besoin de les échanger. -
La paire suivante,
8et5, doit être échangée :3 6 8 5 2 7 4 1 – – 3 6 5 8 2 7 4 1 -
Nous continuons jusqu'à ce que nous atteignions la fin de la liste :
3 6 5 2 8 7 4 1 – – 3 6 5 2 7 8 4 1 – – 3 6 5 2 7 4 8 1 – – 3 6 5 2 7 4 1 8 -
Notre liste n'est pas encore triée, mais nous sommes un peu plus près de la solution parce que la plus grande valeur,
8, a été déplacée complètement vers la droite. -
Nous répétons ceci avec un autre passage sur la liste :
3 6 5 2 7 4 1 8 – – 3 6 5 2 7 4 1 8 – – 3 5 6 2 7 4 1 8 – – 3 5 2 6 7 4 1 8 – – 3 5 2 6 7 4 1 8 – – 3 5 2 6 4 7 1 8 – – 3 5 2 6 4 1 7 8- Notez que nous n'avions pas besoin d'échanger le 3 et le 6, ou le 6 et le 7.
-
Maintenant, la deuxième plus grande valeur,
7, est déplacée complètement vers la droite. Si nous répétons cela, de plus en plus de la liste sera triée et assez rapidement, nous aurons une liste entièrement triée. -
Cet algorithme est appelé tri à bulles, où les grandes valeurs « bullent » vers la droite. Le pseudo-code pour cela pourrait ressembler à :
Répéter n–1 fois Pour i de 0 à n–2 Si le ième et le i+1ème éléments sont désordonnés Les échanger- Puisque nous comparons le ième et le i+1ème élément, nous n'avons besoin d'aller que jusqu'à n – 2 pour
i. Ensuite, nous échangeons les deux éléments s'ils sont désordonnés. - Et nous pouvons arrêter après avoir fait n – 1 passages, puisque nous savons que les n–1 plus grands éléments auront bullé vers la droite.
- Puisque nous comparons le ième et le i+1ème élément, nous n'avons besoin d'aller que jusqu'à n – 2 pour
-
Nous avons n – 2 étapes pour la boucle interne et n – 1 boucles, nous obtenons donc n_2 – 3_n + 2 étapes au total. Mais le plus grand facteur, ou terme dominant, est n_2, car
ndevient de plus en plus grand, donc nous pouvons dire que le tri à bulles est _O(_n_2). - Nous avons vu des temps d'exécution comme ce qui suit, et donc même si la recherche binaire est beaucoup plus rapide que la recherche linéaire, cela pourrait ne pas valoir la peine de trier d'abord la liste, à moins que nous ne fassions beaucoup de recherches au fil du temps :
- O(_n_2)
- Tri à bulles
- O(n log n)
- O(n)
- Recherche linéaire
- O(log n)
- Recherche binaire
- O(1)
- O(_n_2)
- Et Ω pour le tri à bulles est toujours n_2, puisque nous vérifions toujours chaque paire d'éléments pour _n – 1 passages.
Tri par sélection
-
Adoptons une autre approche avec le même ensemble de nombres :
6 3 8 5 2 7 4 1 -
D'abord, examinons chaque nombre et mémorisons le plus petit rencontré. Ensuite, nous pouvons l'échanger avec le premier nombre de notre liste, puisque nous savons que c'est le plus petit :
6 3 8 5 2 7 4 1 – – 1 3 8 5 2 7 4 6 -
Nous savons désormais qu'au moins le premier élément de notre liste est à la bonne place. Nous pouvons donc rechercher le plus petit élément parmi le reste et l'échanger avec l'élément non trié suivant (maintenant le deuxième élément) :
1 3 8 5 2 7 4 6 – – 1 2 8 5 3 7 4 6 -
Nous pouvons répéter cette opération encore et encore, jusqu'à obtenir une liste triée.
-
Cet algorithme est appelé tri par sélection, et voici le pseudo-code que nous pourrions écrire :
Pour i de 0 à n–1 Trouver le plus petit élément entre l'élément ième et le dernier élément Échanger le plus petit élément avec l'élément ième -
Avec la notation O grande, nous avons toujours un temps d'exécution de O(n_2), car nous avons examiné environ tous les _n éléments pour trouver le plus petit, et effectué n passes pour trier tous les éléments.
-
Plus formellement, nous pouvons utiliser certaines formules pour montrer que le plus grand facteur est en effet _n_2 :
n + (n – 1) + (n – 2) + ... + 1 n(n + 1)/2 (n^2 + n)/2 n^2/2 + n/2 O(n^2) -
Il s'avère donc que le tri par sélection fonctionne fondamentalement de la même manière que le tri à bulles en termes de temps d'exécution :
- O(_n_2)
- tri à bulles, tri par sélection
- O(n log n)
- O(n)
- recherche linéaire
- O(log n)
- recherche binaire
- O(1)
- O(_n_2)
- Le meilleur cas, Ω, est également _n_2.
-
Nous pouvons revenir au tri à bulles et modifier son algorithme pour obtenir quelque chose comme ceci, ce qui nous permettra d'arrêter tôt si tous les éléments sont triés :
Répéter jusqu'à ce qu'il n'y ait plus d'échanges Pour i de 0 à n–2 Si les ième et i+1ème éléments ne sont pas dans l'ordre Les échanger- Maintenant, nous n'avons besoin d'examiner chaque élément qu'une seule fois, donc le meilleur cas est maintenant Ω(n) :
- Ω(_n_2)
- tri par sélection
- Ω(n log n)
- Ω(n)
- tri à bulles
- Ω(log n)
- Ω(1)
- recherche linéaire, recherche binaire
- Ω(_n_2)
- Maintenant, nous n'avons besoin d'examiner chaque élément qu'une seule fois, donc le meilleur cas est maintenant Ω(n) :
-
Nous examinons une visualisation en ligne comparaison des algorithmes de tri avec des animations montrant comment les éléments se déplacent dans les tableaux pour le tri à bulles et le tri par sélection.
Récursivité
-
Rappelons que pour la semaine 0, nous avions un pseudo-code pour trouver un nom dans un annuaire téléphonique, où des lignes nous disaient de "revenir en arrière" et de répéter certaines étapes :
1 Prendre l'annuaire téléphonique 2 Ouvrir l'annuaire téléphonique au milieu 3 Regarder la page 4 Si Smith est sur la page 5 Appeler Mike 6 Sinon si Smith est plus tôt dans l'annuaire 7 Ouvrir au milieu de la moitié gauche de l'annuaire 8 **Revenir à la ligne 3** 9 Sinon si Smith est plus tard dans l'annuaire 10 Ouvrir au milieu de la moitié droite de l'annuaire 11 **Revenir à la ligne 3** 12 Sinon 13 Arrêter -
Nous pourrions simplement répéter tout notre algorithme sur la moitié de l'annuaire qu'il nous reste :
1 Prendre l'annuaire téléphonique 2 Ouvrir l'annuaire téléphonique au milieu 3 Regarder la page 4 Si Smith est sur la page 5 Appeler Mike 6 Sinon si Smith est plus tôt dans l'annuaire 7 **Chercher dans la moitié gauche de l'annuaire** 8 9 Sinon si Smith est plus tard dans l'annuaire 10 **Chercher dans la moitié droite de l'annuaire** 11 12 Sinon 13 Arrêter- Cela ressemble à un processus cyclique qui ne finira jamais, mais nous divisons en réalité le problème par deux à chaque fois, et nous arrêtons lorsqu'il n'y a plus d'annuaire.
-
La récursivité se produit lorsqu'une fonction ou un algorithme fait référence à lui-même, comme dans le nouveau pseudo-code ci-dessus.
-
De même, pour la semaine 1, nous avons implémenté une "pyramide" de blocs sous la forme suivante :
# ## ### ####-
Et nous aurions pu avoir un code itératif comme celui-ci :
#include <cs50.h> #include <stdio.h> void draw(int h); int main(void) { // Obtenir la hauteur de la pyramide int height = get_int("Height: "); // Dessiner la pyramide draw(height); } void draw(int h) { // Dessiner une pyramide de hauteur h for (int i = 1; i <= h; i++) { for (int j = 1; j <= i; j++) { printf("#"); } printf("\n"); } }- Ici, nous utilisons des boucles
forpour imprimer chaque bloc de chaque rangée.
- Ici, nous utilisons des boucles
-
-
Mais notez qu'une pyramide de hauteur 4 est en réalité une pyramide de hauteur 3, avec une rangée supplémentaire de 4 blocs ajoutée. Et une pyramide de hauteur 3 est une pyramide de hauteur 2, avec une rangée supplémentaire de 3 blocs. Une pyramide de hauteur 2 est une pyramide de hauteur 1, avec une rangée supplémentaire de 2 blocs. Et enfin, une pyramide de hauteur 1 est juste une pyramide de hauteur 0, ou rien, avec une autre rangée d'un seul bloc ajoutée.
-
Avec cette idée en tête, nous pouvons écrire :
#include <cs50.h> #include <stdio.h> void draw(int h); int main(void) { // Obtenir la hauteur de la pyramide int height = get_int("Height: "); // Dessiner la pyramide draw(height); } void draw(int h) { // Si rien à dessiner if (h == 0) { return; } // Dessiner une pyramide de hauteur h - 1 draw(h - 1); // Dessiner une rangée supplémentaire de largeur h for (int i = 0; i < h; i++) { printf("#"); } printf("\n"); }- Maintenant, notre fonction
drawappelle d'abord elle-même récursivement, dessinant une pyramide de hauteurh - 1. Mais avant même cela, nous devons nous arrêter sihest 0, car il n'y aura plus rien à dessiner. - Ensuite, nous dessinons la rangée suivante, ou une rangée de largeur
h.
- Maintenant, notre fonction
Tri fusion
-
On peut appliquer l'idée de récursion au tri, avec un autre algorithme appelé tri fusion. Voici à quoi pourrait ressembler le pseudo-code :
Si un seul élément Retourner Sinon Trier la moitié gauche des éléments Trier la moitié droite des éléments Fusionner les moitiés triées -
On verra cela plus facilement en pratique avec une liste non triée :
7 4 5 2 6 3 8 1 -
Tout d'abord, on trie la moitié gauche (les quatre premiers éléments) :
7 4 5 2 | 6 3 8 1 – – – – -
Bon, pour trier cela, on doit d'abord trier la moitié gauche de la moitié gauche :
7 4 | 5 2 | 6 3 8 1 – – -
Maintenant, on a juste un élément,
7, dans la moitié gauche, et un élément,4, dans la moitié droite. Donc on fusionnera cela en prenant le plus petit élément de chaque liste en premier :– – | 5 2 | 6 3 8 1 4 7 -
Et maintenant on revient à la moitié droite de la moitié gauche et on la trie :
– – | – – | 6 3 8 1 4 7 | 2 5 -
Maintenant, les deux moitiés de la moitié gauche sont triées, donc on peut fusionner les deux. On regarde le début de chaque liste et on prend
2puisqu'il est plus petit que4. Ensuite, on prend4, puisque c'est maintenant le plus petit élément au début des deux listes. Puis, on prend5, et enfin7, pour obtenir :– – – – | 6 3 8 1 – – – – 2 4 5 7 -
Maintenant on trie la moitié droite de la même manière. D'abord, la moitié gauche de la moitié droite :
– – – – | – – | 8 1 – – – – | 3 6 | 2 4 5 7 -
Ensuite, la moitié droite de la moitié droite :
– – – – | – – | – – – – – – | 3 6 | 1 8 2 4 5 7 -
On peut maintenant fusionner la moitié droite :
– – – – | – – – – – – – – | – – – – 2 4 5 7 | 1 3 6 8 -
Enfin, on peut fusionner les deux moitiés de la liste entière en suivant les mêmes étapes que précédemment. Remarquez que nous n'avons pas besoin de vérifier tous les éléments de chaque moitié pour trouver le plus petit, puisque nous savons que chaque moitié est déjà triée. Au lieu de cela, il suffit de prendre le plus petit élément sur deux au début de chaque moitié :
– – – – | – – – – – – – – | – – – – 2 4 5 7 | – 3 6 8 1 – – – – | – – – – – – – – | – – – – – 4 5 7 | – 3 6 8 1 2 – – – – | – – – – – – – – | – – – – – 4 5 7 | – – 6 8 1 2 3 – – – – | – – – – – – – – | – – – – – – 5 7 | – – 6 8 1 2 3 4 – – – – | – – – – – – – – | – – – – – – – 7 | – – 6 8 1 2 3 4 5 – – – – | – – – – – – – – | – – – – – – – 7 | – – – 8 1 2 3 4 5 6 – – – – | – – – – – – – – | – – – – – – – – | – – – 8 1 2 3 4 5 6 7 – – – – | – – – – – – – – | – – – – – – – – | – – – – 1 2 3 4 5 6 7 8 -
Il y a pas mal d'étapes, mais en réalité il en faut moins que pour les autres algorithmes vus jusqu'à présent. On divise la liste en deux à chaque fois, jusqu'à "trier" huit listes avec un seul élément chacune :
7 | 4 | 5 | 2 | 6 | 3 | 8 | 1 4 7 | 2 5 | 3 6 | 1 8 2 4 5 7 | 1 3 6 8 1 2 3 4 5 6 7 8 -
Comme notre algorithme divise le problème en deux à chaque fois, sa durée d'exécution est logarithmique, avec O(log n). Après avoir trié chaque moitié (ou la moitié d'une moitié), on assemble tous les éléments, en n étapes, puisque l'on doit regarder chaque élément une fois.
- La durée d'exécution totale est donc O(n log n) :
- O(n²)
- tri à bulles, tri par sélection
- O(n log n)
- tri fusion
- O(n)
- recherche linéaire
- O(log n)
- recherche dichotomique
- O(1)
- O(n²)
- Comme log n est supérieur à 1 mais inférieur à n, n log n se situe entre n (fois 1) et n².
- Le meilleur cas, Ω, reste n log n, puisqu'on continue à trier chaque moitié d'abord puis à les fusionner :
- Ω(n²)
- tri par sélection
- Ω(n log n)
- tri fusion
- Ω(n)
- tri à bulles
- Ω(log n)
- Ω(1)
- recherche linéaire, recherche dichotomique
- Ω(n²)
- Enfin, il y a une autre notation, Θ, Theta, que l'on utilise pour décrire les durées d'exécution des algorithmes si la borne supérieure et la borne inférieure sont identiques. Par exemple, le tri fusion est noté Θ(n log n) puisque le meilleur et le pire cas nécessitent le même nombre d'étapes. Et le tri par sélection est Θ(n²).
- On regarde une visualisation finale des algorithmes de tri avec un plus grand nombre d'entrées, exécutés en même temps.