Séance 5

• Pointeurs
• Redimensionnement de tableaux
• Structures de données
• Listes chaînées
• Autres structures de données

Pointeurs

• La dernière fois, nous avons appris les pointeurs, malloc, et d’autres outils utiles pour travailler avec la mémoire.

• Révisons ce bout de code :

    int main(void)
    {
        int *x;
        int *y;
  
        x = malloc(sizeof(int));
  
        *x = 42;
        *y = 13;
    }
  

  • Ici, les deux premières lignes de code dans notre fonction main déclarent deux pointeurs, x et y. Puis, nous allouons assez de mémoire pour un int avec malloc, et stockons l’adresse retournée par malloc dans x.
  • Avec *x = 42;, nous allons à l’adresse pointée par x et y stockons la valeur 42 à cet emplacement.

  • La dernière ligne, cependant, est boguée, puisque nous ne savons pas quelle est la valeur de y, puisque nous ne lui avons jamais attribué de valeur. À la place, nous pouvons écrire :

      y = x;
      *y = 13;
    

    • Et ceci fera pointer y sur le même emplacement que x, et ensuite attribuera la valeur 13 à cet emplacement.

• Nous jetons un œil à un court clip, Pointer Fun with Binky, qui explique aussi ce bout de code de manière animée !

Redimensionnement de tableaux

• Au cours de la semaine 2, nous avons appris sur les tableaux, où nous pouvions stocker le même type de valeur dans une liste, côte à côte. Mais nous devons déclarer la taille des tableaux lorsque nous les créons, et lorsque nous voulons augmenter la taille du tableau, la mémoire qui l'entoure peut être occupée par d'autres données.
• Une solution pourrait être d'allouer plus de mémoire dans une zone plus grande qui est libre, et d'y déplacer notre tableau, où il a plus d'espace. Mais nous devrons copier notre tableau, ce qui devient une opération avec un temps d'exécution de O(n), car nous devons copier chacun des n éléments dans un tableau.

• Nous pourrions écrire un programme comme celui qui suit, pour le faire dans le code :

    #include <stdio.h>
    #include <stdlib.h>
  
    int main(void)
    {
        // Ici, nous allouons suffisamment de mémoire pour accueillir trois entiers, et notre variable
        // list pointera vers le premier entier.
        int *list = malloc(3 * sizeof(int));
        // Nous devrions vérifier que nous avons correctement alloué de la mémoire, car malloc pourrait
        // ne pas obtenir suffisamment de mémoire libre.
        if (list == NULL)
        {
            return 1;
        }
  
        // Avec cette syntaxe, le compilateur effectuera l'arithmétique des pointeurs pour nous, et
        // calculera l'octet en mémoire auquel list[0], list[1] et list[2] sont mappés,
        // puisque les entiers font 4 octets.
        list[0] = 1;
        list[1] = 2;
        list[2] = 3;
  
        // Maintenant, si nous voulons redimensionner notre tableau pour accueillir 4 entiers, nous allons essayer d'allouer
        // suffisamment de mémoire pour eux, et utiliser temporairement tmp pour pointer vers le premier :
        int *tmp = malloc(4 * sizeof(int));
        if (tmp == NULL)
        {
            return 1;
        }
  
        // Maintenant, nous copions les entiers de l'ancien tableau dans le nouveau tableau ...
        for (int i = 0; i < 3; i++)
        {
            tmp[i] = list[i];
        }
  
        // ... et ajoutons le quatrième entier :
        tmp[3] = 4;
  
        // Nous devrions libérer la mémoire d'origine pour list, c'est pourquoi nous avons besoin d'une
        // variable temporaire pour pointer vers le nouveau tableau ...
        free(list);
  
        // ... et maintenant nous pouvons définir notre variable list pour qu'elle pointe vers le nouveau tableau que
        // tmp indique :
        list = tmp;
  
        // Maintenant, nous pouvons imprimer le nouveau tableau :
        for (int i = 0; i < 4; i++)
        {
            printf("%i\n", list[i]);
        }
  
        // Et enfin, libérer la mémoire du nouveau tableau.
        free(list);
    }
  

• Il s'avère qu'il existe en fait une fonction utile, realloc, qui réallouera de la mémoire :

    #include <stdio.h>
    #include <stdlib.h>
  
    int main(void)
    {
        int *list = malloc(3 * sizeof(int));
        if (list == NULL)
        {
            return 1;
        }
  
        list[0] = 1;
        list[1] = 2;
        list[2] = 3;
  
        // Ici, nous donnons à realloc notre tableau d'origine sur lequel list pointe, et il
        // renverra une nouvelle adresse pour un nouveau tableau, avec les anciennes données copiées :
        int *tmp = realloc(list, 4 * sizeof(int));
        if (tmp == NULL)
        {
            return 1;
        }
        // Maintenant, tout ce que nous avons à faire est de mémoriser l'emplacement du nouveau tableau :
        list = tmp;
  
        list[3] = 4;
  
        for (int i = 0; i < 4; i++)
        {
            printf("%i\n", list[i]);
        }
  
        free(list);
    }
  

Structures de données

• Les Structures de données sont des structures de programmation qui nous permettent de stocker des informations selon différentes dispositions, dans la mémoire de notre ordinateur.
• Pour construire une structure de données, nous allons utiliser quelques outils que nous avons vu :
  • struct pour créer des types de données personnalisés
  • . pour accéder aux propriétés d'une structure
  • * pour aller à une adresse en mémoire pointée par un pointeur

Listes chaînées

• Avec une liste chaînée, nous pouvons stocker une liste de valeurs qui peut facilement être étendue en stockant des valeurs dans différentes parties de la mémoire :

  

  • C’est différent d’un tableau car nos valeurs ne sont plus les unes à côté des autres en mémoire.

• Nous pouvons lier notre liste ensemble en allouant, pour chaque élément, suffisamment de mémoire pour la valeur que nous voulons stocker, et pour l’adresse de l’élément suivant :

  

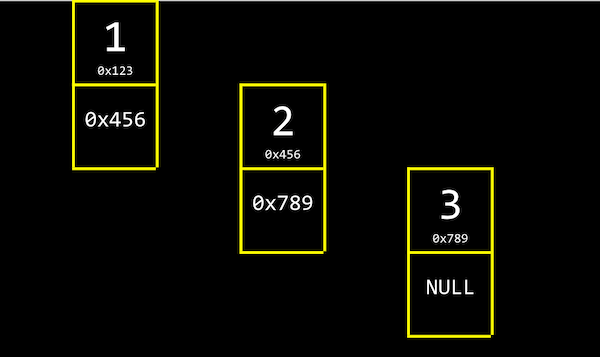
  • Au fait, NUL fait référence à \0, un caractère qui termine une chaîne de caractères, et NULL fait référence à une adresse de tous les zéros, ou un pointeur nul que nous pouvons considérer comme pointant vers nulle part.

• Contrairement à ce que nous pouvons faire avec des tableaux, nous n’avons plus accès aléatoire aux éléments d’une liste chaînée. Par exemple, nous ne pouvons plus accéder au 5e élément de la liste en calculant où il se trouve, en temps constant. (Sachant que les tableaux stockent les éléments bout à bout, nous pouvons ajouter 1, ou 4, ou la taille de notre élément, pour calculer les adresses.) Au lieu de cela, nous devons suivre le pointeur de chaque élément, un à la fois. Et nous devons allouer deux fois plus de mémoire que nécessaire auparavant pour chaque élément.

• En code, nous pouvons créer notre propre structure appelée node (comme un nœud d’un graphe en mathématiques), et nous devons stocker à la fois un int et un pointeur vers le prochain node appelé next :

    typedef struct node
    {
        int number;
        struct node *next;
    }
    node;
  

  • Nous commençons cette structure par typedef struct node de sorte que nous puissions faire référence à un node à l’intérieur de notre structure.

• Nous pouvons construire une liste chaînée en code en commençant par notre structure. Tout d’abord, nous allons vouloir nous souvenir d’une liste vide, nous pouvons donc utiliser le pointeur null : node *list = NULL;.

• Pour ajouter un élément, nous aurons d’abord besoin d’allouer de la mémoire pour un nœud et de définir ses valeurs :

    node *n = malloc(sizeof(node));
    // Nous voulons nous assurer que malloc a réussi à obtenir de la mémoire pour nous :
    if (n != NULL)
    {
        // Cela équivaut à (*n).number, où nous allons d'abord au nœud pointé
        // par n, puis définissons la propriété number. En C, nous pouvons également
        // utiliser cette notation de flèche :
        n->number = 2;
        // Ensuite, nous devons stocker un pointeur vers le nœud suivant de notre liste,
        // mais le nouveau nœud ne pointera vers rien (pour l’instant) :
        n->next = NULL;
    }
  

• Maintenant, notre liste peut pointer vers ce nœud : list = n; :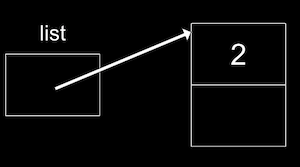

  

• Pour ajouter à la liste, nous allons créer un nouveau nœud de la même manière, peut-être avec la valeur 4. Mais maintenant, nous devons mettre à jour le pointeur dans notre premier nœud pour qu’il y pointe.

• Étant donné que notre pointeur list pointe uniquement vers le premier nœud (et nous ne pouvons pas être sûrs que la liste ne comporte qu’un seul nœud), nous devons « suivre les miettes de pain » et suivre le pointeur suivant de chaque nœud :

    // Créer un pointeur temporaire vers ce que pointe list
    node *tmp = list;
    // Tant que le nœud a un pointeur suivant ...
    while (tmp->next != NULL)
    {
        // ... définir le temporaire au nœud suivant
        tmp = tmp->next;
    }
    // Maintenant, tmp pointe vers le dernier nœud de notre liste, et nous pouvons mettre
    // à jour son pointeur suivant pour qu'il pointe vers notre nouveau nœud.
  

• Si nous voulons insérer un nœud au début de notre liste chaînée, nous devons soigneusement mettre à jour notre nœud pour qu’il pointe vers celui qui le suit, avant de mettre à jour la liste. Sinon, nous perdrons le reste de notre liste :

    // Ici, nous insérons un nœud au début de la liste, nous voulons donc que son
    // pointeur suivant pointe vers la liste d'origine, avant de pointer la liste vers
    // n :
    n->next = list;
    list = n;
  

• Et pour insérer un nœud au milieu de notre liste, nous pouvons parcourir la liste, en suivant chaque élément un à la fois, en comparant ses valeurs et en modifiant également avec soin les pointeurs next.

• Avec quelques volontaires sur scène, nous simulons une liste, chaque volontaire agissant comme la variable list ou un nœud. Au fur et à mesure que nous insérons des nœuds dans la liste, nous avons besoin d’un pointeur temporaire pour suivre la liste et nous assurer de ne perdre aucune partie de notre liste. Notre liste chaînée ne pointe que vers le premier nœud de notre liste, nous ne pouvons donc regarder qu'un nœud à la fois, mais nous pouvons allouer dynamiquement plus de mémoire au fur et à mesure que nous devons agrandir notre liste.

• Désormais, même si notre liste chaînée est triée, le temps de recherche sera de O(n), car nous devons parcourir chaque nœud afin de vérifier ses valeurs et nous ne savons pas où se situe le milieu de notre liste.

• Nous pouvons combiner tous nos fragments de code en un programme complet :

    #include <stdio.h>
    #include <stdlib.h>
  
    // Représente un nœud
    typedef struct node
    {
        int number;
        struct node *next;
    }
    node;
  
    int main(void)
    {
        // Liste de taille 0, qui ne pointe initialement vers rien
        node *list = NULL;
  
        // Ajouter un nombre à la liste
        node *n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = 1;
        n->next = NULL;
        // Nous créons notre premier nœud, y stockons la valeur 1 et laissons le pointeur suivant pointer vers rien. Ensuite, notre variable de liste peut y pointer.
        list = n;
  
        // Ajouter un nombre à la liste
        n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = 2;
        n->next = NULL;
        // Maintenant, nous allons à notre premier nœud pointé par list, et nous définissons le pointeur suivant pour qu'il pointe vers notre nouveau nœud, ajoutant ainsi celui-ci à la fin de la liste :
        list->next = n;
  
        // Ajouter un nombre à la liste
        n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = 3;
        n->next = NULL;
        // Nous pouvons suivre plusieurs nœuds avec cette syntaxe, en utilisant le pointeur suivant encore et encore pour ajouter notre troisième nouveau nœud à la fin de la liste :
        list->next->next = n;
        // Normalement, nous voudrions toutefois une boucle et une variable temporaire pour ajouter un nouveau nœud à notre liste.
  
        // Imprimer la liste
        // Ici, nous pouvons itérer sur tous les nœuds de notre liste avec une variable temporaire. Tout d'abord, nous avons un pointeur temporaire, tmp, qui pointe vers la liste. Ensuite, notre condition pour continuer est que tmp ne soit pas NULL. Enfin, nous mettons à jour tmp sur le pointeur suivant :
        for (node *tmp = list; tmp != NULL; tmp = tmp->next)
        {
            // Dans le nœud, nous imprimerons simplement le nombre stocké :
            printf("%i\n", tmp->number);
        }
  
        // Libérer la liste
        // Comme nous libérons chaque nœud au fur et à mesure, nous allons utiliser une boucle while et suivrons le pointeur suivant de chaque nœud avant de le libérer. Toutefois, nous verrons cela plus en détail dans le problème n° 5.
        while (list != NULL)
        {
            node *tmp = list->next;
            free(list);
            list = tmp;
        }
    }
  

Plus de structures de données

• Un arbre est une autre structure de données où chaque nœud pointe vers deux autres nœuds, un à gauche (avec une valeur plus petite) et un à droite (avec une valeur plus grande) :
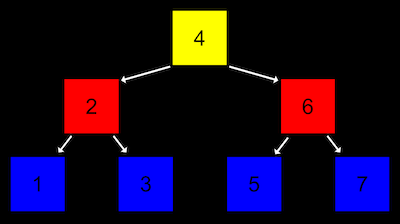
  • Notez qu'il y a maintenant deux dimensions dans cette structure de données, où certains nœuds sont à des « niveaux » différents des autres. Et nous pouvons imaginer l'implémenter avec une version plus complexe d'un nœud dans une liste chaînée, où chaque nœud n'a pas un mais deux pointeurs, un vers la valeur au « milieu de la moitié gauche » et un vers la valeur au « milieu de la moitié droite ». Et tous les éléments à gauche d'un nœud sont plus petits, et tous les éléments à droite sont plus grands.
  • Ceci est appelé un arbre de recherche binaire parce que chaque nœud a au plus deux enfants, ou nœuds vers lesquels il pointe, et un arbre de recherche parce qu'il est trié d'une manière qui nous permet de rechercher correctement.
  • Et comme une liste chaînée, nous voudrons garder un pointeur juste au début de la liste, mais dans ce cas, nous voulons pointer vers la racine, ou nœud central supérieur de l'arbre (le 4).

• Maintenant, nous pouvons facilement faire une recherche binaire, et puisque chaque nœud pointe vers un autre, nous pouvons également insérer des nœuds dans l'arbre sans avoir à les déplacer tous comme nous aurions à le faire dans un tableau. La recherche récursive de cet arbre ressemblerait à ceci :

    typedef struct node
    {
        int number;
        struct node *left;
        struct node *right;
    } node;
  
    // Ici, *tree est un pointeur vers la racine de notre arbre.
    bool search(node *tree)
    {
        // Nous avons besoin d'un cas de base, si l'arbre courant (ou une partie de l'arbre) est NULL,
        // pour renvoyer faux :
        if (tree == NULL)
        {
            return false;
        }
        // Maintenant, selon que le nombre dans le nœud courant est plus grand ou plus petit,
        // on peut simplement regarder le côté gauche ou droit de l'arbre :
        else if (50 < tree->number)
        {
            return search(tree->left);
        }
        else if (50 > tree->number)
        {
            return search(tree->right);
        }
        // Sinon, le nombre doit être égal à celui que nous recherchons :
        else {
            return true;
        }
    }
  

• Le temps d'exécution pour rechercher dans un arbre est O(log n), et l'insertion de nœuds tout en maintenant l'arbre équilibré est également O(log n). En dépensant un peu plus de mémoire et de temps pour maintenir l'arbre, nous avons maintenant gagné en rapidité pour les recherches par rapport à une liste chaînée simple.

• Une structure de données avec un temps de recherche presque constant est une table de hachage, qui est une combinaison d'un tableau et d'une liste chaînée. Nous avons un tableau de listes chaînées, et chaque liste chaînée dans le tableau contient des éléments d'une certaine catégorie. Par exemple, dans le monde réel, nous pourrions avoir beaucoup de badges nominaux, et nous pourrions les trier en 26 compartiments, chacun étiqueté avec une lettre de l'alphabet, afin de pouvoir trouver les badges en regardant simplement dans un compartiment.
• Nous pouvons implémenter cela dans une table de hachage avec un tableau de 26 pointeurs, chacun pointant vers une liste chaînée pour une lettre de l'alphabet :
  
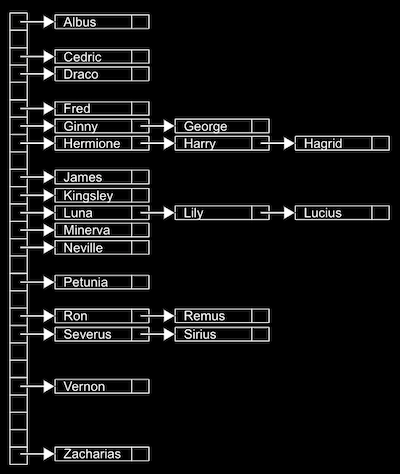
• Étant donné que nous avons un accès aléatoire avec les tableaux, nous pouvons ajouter des éléments rapidement et aussi indexer rapidement dans un compartiment.
• Un compartiment peut contenir plusieurs valeurs correspondantes, nous utiliserons donc une liste chaînée pour stocker toutes les valeurs horizontalement. (Nous appelons cela une collision, lorsque deux valeurs correspondent d'une certaine manière.)
• Cela s'appelle une table de hachage parce que nous utilisons une fonction de hachage, qui prend une entrée et la mappe dans un compartiment où elle doit aller. Dans notre exemple, la fonction de hachage se contente de regarder la première lettre du nom, donc elle pourrait retourner 0 pour "Albus" et 25 pour "Zacharias".
• Mais dans le pire des cas, tous les noms pourraient commencer par la même lettre, donc nous pourrions nous retrouver avec l'équivalent d'une seule liste chaînée. Nous pourrions examiner les deux premières lettres et allouer suffisamment de compartiments pour 26*26 valeurs hachées possibles, ou même les trois premières lettres, et maintenant nous aurions besoin de 26*26*26 compartiments. Mais nous pourrions encore avoir un pire cas où toutes nos valeurs commencent par les mêmes trois caractères, donc le temps d'exécution pour la recherche est O(n). En pratique, cependant, nous pouvons nous rapprocher de O(1) si nous avons à peu près autant de compartiments que de valeurs possibles, surtout si nous avons une fonction de hachage idéale, où nous pouvons trier nos entrées dans des compartiments uniques.
• Nous pouvons utiliser une autre structure de données appelée trie (se prononce comme “try”, et est l'abréviation de “retrieval”) :
  
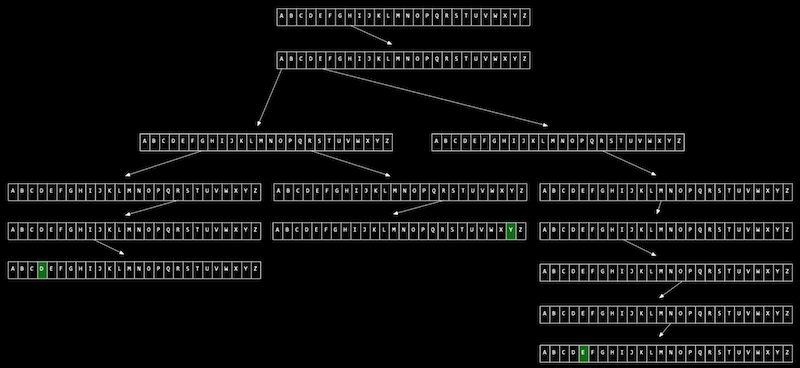
  • Imaginez que nous voulons stocker un dictionnaire de mots de manière efficace et être capable d'accéder à chacun d'eux en temps constant. Un trie est comme un arbre, mais chaque nœud est un tableau. Chaque tableau contiendra chaque lettre, de A à Z. Pour chaque mot, la première lettre pointera vers un tableau, où la lettre suivante valide pointera vers un autre tableau, et ainsi de suite, jusqu'à ce que nous atteignions quelque chose indiquant la fin d'un mot valide. Si notre mot n'est pas dans le trie, alors l'un des tableaux ne contiendra pas de pointeur ou de caractère de terminaison pour notre mot. Maintenant, même si notre structure de données contient beaucoup de mots, le temps de recherche sera juste la longueur du mot que nous recherchons, et cela pourrait être un maximum fixe donc nous avons O(1) pour la recherche et l'insertion. Le coût pour cela, cependant, est 26 fois plus de mémoire que ce dont nous avons besoin pour chaque caractère.
• Il existe des constructions encore plus complexes, les structures de données abstraites, où nous utilisons nos blocs de construction de tableaux, listes chaînées, tables de hachage et tries pour implémenter une solution à un problème donné.
• Par exemple, une structure de données abstraite est une queue, où nous voulons pouvoir ajouter des valeurs et en supprimer dans un ordre premier entré, premier sorti (FIFO). Pour ajouter une valeur, nous pourrions l’enfiler, et pour en retirer une, nous la décongestionnerions. Et nous pouvons l'implémenter avec un tableau que nous redimensionnons à mesure que nous ajoutons des éléments, ou une liste chaînée où nous ajoutons des valeurs à la fin.
• Une structure de données “opposée” serait une pile, où les éléments les plus récemment ajoutés (empilés) sont supprimés (dépilés) en premier, dans un ordre dernier entré, premier sorti (LIFO). Notre boîte de réception d'e-mails est une pile, où nos e-mails les plus récents sont en haut.
• Un autre exemple est un dictionnaire, où nous pouvons mapper des clés à des valeurs, ou des chaînes à des valeurs, et nous pouvons en implémenter un avec une table de hachage où un mot est associé à d'autres informations (comme sa définition ou son sens).
• Nous jetons un œil à “Jack Learns the Facts About Queues and Stacks”, une animation sur ces structures de données.